令 \(f(0)=0,\ f(1)=1\),以及 \(f(n)=f(n-1)+f(n-2),\ \forall n>1\)。輸入非負整數 \(n\),請輸出 \(f(n)\) 除以 \(p\) 的餘數, \(p=1e9+7\)。\(n<231\)
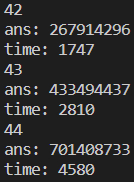
遞迴(Slowest)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
# include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int p = 1e9+7;
ll f(ll n){
if(n == 0) return 0;
if(n == 1) return 1;
return (f(n-1) + f(n-2)) % p;
}
int main(){
ll n;
while(cin>>n){
// clock_t a, b;
// a = clock();
cout << "ans: " << f(n) << '\n';
// b = clock();
// cout << "time: " << b-a << '\n';
}
return 0;
}
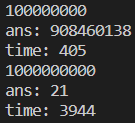
迴圈(\(O(n)\))
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
# include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int p = 1e9+7;
int main(){
ll n;
ll a, b, c;
while(cin>>n){
// clock_t x, y;
// x = clock();
a = 0;
b = 1;
for(ll i=2; i<=n; i++){
c = (a + b) % p;
a = b;
b = c;
}
cout << "ans: " << c << '\n';
// y = clock();
// cout << "time: " << y-x << '\n';
}
return 0;
}
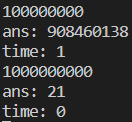
矩陣快速冪(\(O(log\ n)\))
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
# include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int p = 1e9+7;
struct matrix{
ll mat[2][2];
// initialized
void init(ll a, ll b, ll c, ll d){
mat[0][0] = a;
mat[0][1] = b;
mat[1][0] = c;
mat[1][1] = d;
return;
}
};
// matrix multiply
matrix mul(matrix A, matrix B){
matrix ANS;
ANS.init(0, 0, 0, 0);
for(int i=0; i<2; i++){
for(int j=0; j<2; j++){
for(int k=0; k<2; k++) ANS.mat[i][j] += (A.mat[i][k] * B.mat[k][j]) % p;
ANS.mat[i][j] %= p;
}
}
return ANS;
}
matrix exp(matrix A, ll n){
if(n == 1) return A;
if(n & 1) return mul(exp(A, n-1), A);
matrix TMP;
TMP.init(0, 0, 0, 0);
TMP = exp(A, n/2);
return mul(TMP, TMP);
}
int main(){
ll n;
matrix A;
A.init(1, 1, 1, 0);
while(cin>>n && n!=-1){
clock_t a, b;
a = clock();
cout << "ans: " << exp(A, n-1).mat[0][0] % p << '\n';
b = clock();
cout << "time: " << b-a << '\n';
}
return 0;
}